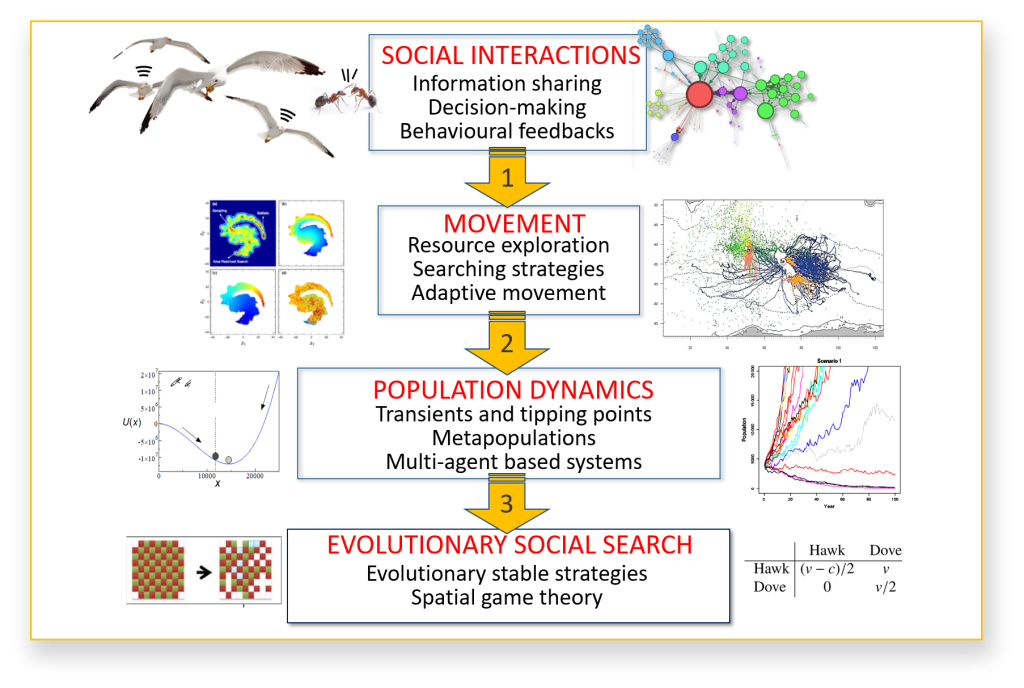
Information on the relevant global scales of the search space, even if partial, should conceivably enhance the performance of random searches.
Here we show numerically and analytically that the paradigmatic uninformed optimal Lévy searches can be outperformed by informed multiple-scale random searches in one (1D) and two (2D) dimensions, even when the knowledge about the relevant landscape scales is incomplete. We show in the low-density nondestructive regime that the optimal efficiency of biexponential searches that incorporate all key scales of the 1D landscape of size L decays asymptotically as ηopt∼1/√L, overcoming the result ηopt∼1/(√LlnL) of optimal Lévy searches.
We further characterize the level of limited information the searcher can have on these scales. We obtain the phase diagram of bi- and triexponential searches in 1D and 2D. Remarkably, even for a certain degree of lack of information, partially informed searches can still outperform optimal Lévy searches. We discuss our results in connection with the foraging problem.